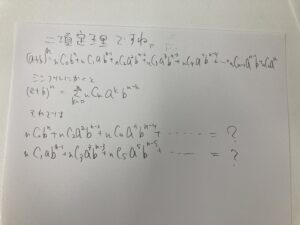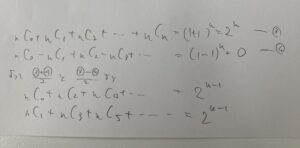二項定理の応用。
松谷です。
たまには?数学の話題でも。
さて二項定理というやつがあります。
(a+b)^nを展開した式ですね。
シグマできれいにかかれていますが、案外、展開した方が内容がつかみやすいという面もあります。
aの2乗×bの(n-2)乗の係数は、(a+b)のn個の箱からaを取り出す箱を二つ選ぶと考えたら係数がnC2になることは当たり前ですね。
だからそれを書き並べただけです。(あっ参考書にはaのn-k乗、bのk乗の順番で書いていた…。その方が良かったか。。。。)
では書き並べた中で、偶数番目のものを取り出した和、奇数番目だけ取り出した和はどう表せるでしょうか?
それは少し考えてしまうかもしれません。
少し難しい題材を考えるとき、似たような経験がないかと自分のなかを検索するのはひとつの重要な手法かなと思います。
そうしたら、ああこんな内容がありましたね。
いや、まあないかもしれませんが。。一応常識だと思っておいてください。
でよく考えたら、これを一般化しているだけなわけですね。
はい。奇数番目は(-a)のk乗が-(aのk乗)になって、偶数番目は、(-a)のk乗が(aのk乗)になることを利用して、同じようにすればいいですね!
これのa=1,b=1の例が最初に思い出した類似の話ですね!
(やっぱり最初の公式の記述を逆にしておけば良かった。。。でもまあ少し違った見た目にも対応できるのは大事!としておきたいと思います。。)
生徒の答案を採点していて、その方針だと行き詰っていましたが、この知識を利用したら突破できるなと思って書いてみました。
まあ、本当は漸化式を立てるのが最適解だったのですが、行き詰った方針にも学びがあったりするんですよね。