新年初数学、算数？

松谷です。

12/30と12/31と1/1は子供と遊ぶ以外は読書をしていたので、

新年初めて、数学らしいものに触れました。

それがこれですね。

共通テストも近いので、生徒の気持ちになるべく近づくために、共通テストだけやたら問われるので図形問題について少しだけ見ておこうと思いまして。

実際はセンター試験の時と変わらずよく出る構図ですが。

 

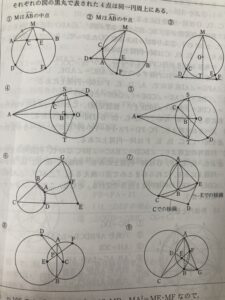
これが同一円周上にあることを言うときに何が注意かというと、

①直角三角形の中にある相似と、②方べきの定理、そして③方べきの定理の逆

という2次試験でほとんど問われないのに共通テストで頻繁に問われる3つが全部入ってるからですね。

しかもベクトルや図形と方程式でも重要な反転の構図にもなってますしね。

 

当時、こういうのを一瞬で分からなくてショックを受けたのを思い出します。

しかし、結局構図として、見たことがあること。そして、上の①②③とか(今回は関係ないですがあとチェバメネラウスとかも)が結構問われるんだよ。

という予備知識があればまあそんなにたいしたことはないわけですね。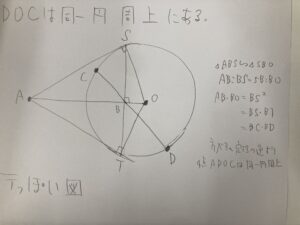　

 

正月の頭の体操にはいいですよね！

こういうのっていっぱいありますね！

予備知識なしだと上の9つやるだけで最初は1時間とか下手したらもっとかかってしまうかもしれないですが、メタ的な知識を知っていてかなり慣れてくれば10分以内くらいでできてもおかしくないんですよね。

図形的に4点が円周上にあることを示すならば、円周角の定理の逆、四角形の対角の和180°(とその変形の外角とその内対角が等しい。特に2直角で180°)、方べきの定理の逆、まあそんなもんですからね。計算系統だと中心からの半径が等しいとか、複素数平面上で検討するとかもありえるでしょうけど。