よくある問題に見えるが
松谷です。
ゴールデンウィークですね。
いかがお過ごしでしょうか?
僕もリラックスしてます。
そんなときにふと思い浮かんだ問題があったんですね。
図形の周りを円がすべらずに転がる問題ってありますよね。
小、中学生あたりだとよくあります。
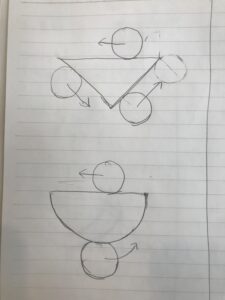
たとえば、
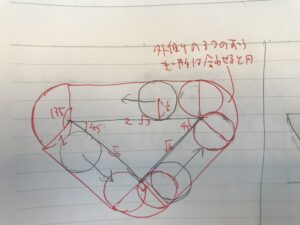
上であれば、一辺√6の直角二等辺三角形の外を半径1/2の円を転がすときの円が通過する面積を求めよ。
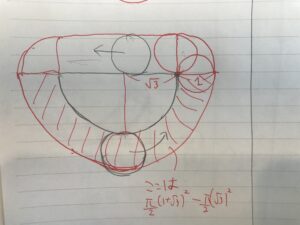
下であれば、半径√3の半円の外側を半径1/2の円を転がすときの円が通過する面積を求めよ。
みたいな。
そんな感じでしたら、面積は出せますね。
こんな感じですね。
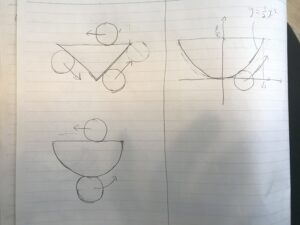
でも、それを拡張させて中の図形をちょっと違うものに変えるとどうでしょう。
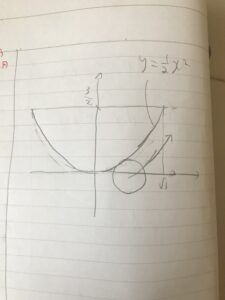
中を放物線に蓋がある図形にしてみました。そうすると、うーむ。
簡単そうで全然簡単じゃなさそうですね。
特に放物線の下側を転がる図形の面積の計算が結構辛そうですね。(媒介変数表示してから数3の置換積分を使ってやる方法が思い浮かびましたが、、もっと簡単なやり方があるのかもしれませんが。。)
こんな感じで、少しだけ問題を掘ってみるだけでもいろいろな発見がありますね。それが高校数学の範囲で解けるかどうかはともかくね。