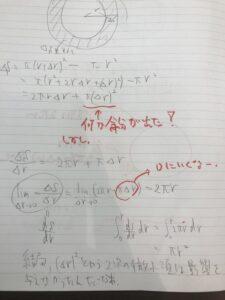素朴な数学のギモン。
松谷です。
素朴な数学のギモンをふと思うときってありますよね。
僕は昔こんなのギモンに思うことありました。
なんか、これほんとなのかな。
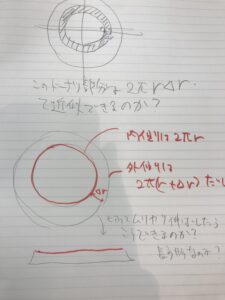
これが近似できるなら積分したら円の面積がπr^2ってなりそうだけど。
でも、なんか円周の長さ内側と外側でちょっと違う気もするから単純に近似できるんかいな。。みたいな。
結論から言うとokなのですが、ドーナツ型の面積を外の面積から中の面積を引いて求めてあげたらもう少し疑問の中身がわかるとおもいます。
つまり、2次の微小項が△rで割ってから極限とったときに0になるので関係なかったわけですね。
なんだ結局関係なかったからいいやいいや。
と思うんですが、
こんな考察がガチガチのハイレベル受験の前の考察としては有用なんですね。
つまり、半径1の球の表面積を求めるときの、横に輪切りにしたときの面積の増えた分ΔSを2π√(1-r)^2Δrで近似していいのかみたいなやつです。結論これはだめなんですが、そういうのに繋がっていくかなと。