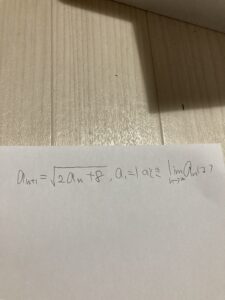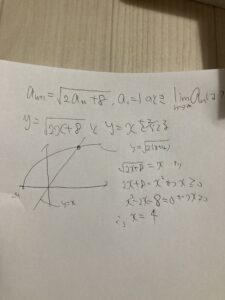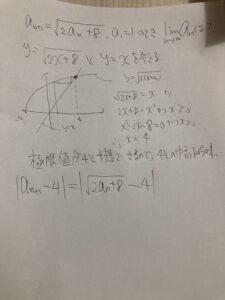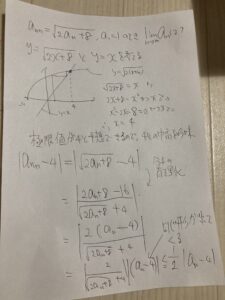解けない漸化式の極限。ここからどうする？

松谷です。

解けない漸化式の極限を求める問題ってあるんですよね。

 

こういうやつです。漸化式は解けないのに極限が求まるってことがあるわけですね。

グラフなどで極限値を予想してはさみうちの原理で示すって流れが典型的な流れです。

この問題だったら、

y=√2x+8とy=xとその交点を考えるんです。

これだと交点のx座標が4ってわかります。

これらを考えることで、視覚的にa1,a2,a3・・・の決まり方がわかるんですね。

ざっくりいうと、y=√2x+8のxにa1を代入したらyとしてa2が出てきてそれをx座標に移すためにy=xを持ち出してるわけです。

階段を書くみたいな感じですね。そうしたら、極限値が4と予想できました。

あとは、4との幅を吟味します。つまりan+1と4の幅が、anと4の幅より狭まっていれば最終的にどんどん狭まっていき、4に収束するじゃん！っていうのをはさみうちの原理で示していくんですね。

はい。こんな感じで示していくんですね。

典型的なので最後までは書きません。慣れれば誰でもできると思います。

 

しかしながら、

 

途中で、分子の有理化してますよね。

 

これなんでですかね？

 

 

いやそういうもんやねん。

引くやつに極限値をもってきといて、分子の有理化してら、

|an-4|の形が引っ張り出せるねん。

そんな説明をするのが普通です。もしくは説明しない方が普通かもしれません。

 

でも、分子の有理化が出来ず止まってる人がほんの少しながらいて、何回もやった技術をなぜ使えるようになってくれないんだと悲しい気持ちになったんですね。

 

でも、それと同時に思いました。

まあ、因果関係ないものを引っ張り出せないときあるよなあと。

 

まあこれは、実際は平均値の定理とかを使っても無理やり|an-4|の形を引っ張り出せるんですが、有理化でやっていつも引っ張れるのかというのを一般的に考えて見るのも面白いかなと。

 

ということで、やってみました。an+1=√f(an)でf(x)は整式とします。

するとどうでしょうか。

 

おっ、一般的に上手くいくことが示されましたね！

有理化して、分子からルートがとれて整式がやってきたときに、因数定理から、an-αが引っ張り出せるわけですね〜。

 

なるほどなるほど。

どこの本にもサイトにも載ってなかった気がしたので、小さな発見か！！いやしょーもなすぎて誰も考えなかっただけなんでしょうね。。

 

まあいいか。

記事を一本稼げたということが1番大事なわけですね笑

 

ではよい休日をお過ごしください！