標準正規分布の期待値を積分で求める！

松谷です。

統計が今年の高1生から課程に入っています。

その中のおそらく最重要であるものとして、

正規分布というものがあります。

共通テストの点数の分布だけでなく、身長の分布、工場などで作る規定のねじなどの誤差を測る分布、何より標本平均の分布（中心極限定理）などとして大いに活躍します。

で、その正規分布曲線自体は、それはいろんなものを表すときに異なったグラフになるのですが、それらに変換をかましてやると全部が

標準正規分布というものになるわけですね。N(0,1)などと書いたりします。

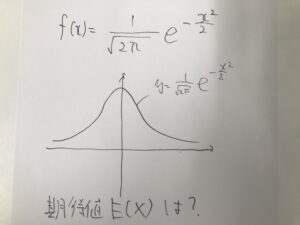
標準正規分布を表す関数は、じゃん

こんな感じの関数で表されるんですね。グラフはこんな感じですね。真ん中に0が来ているなあ、y軸対称っぽいなあということが感じられると思います。

y軸対称だなあというのは、x→-xとしたら一緒の式ですから偶関数ですから当たり前ですね。

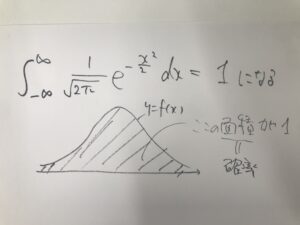
で、この関数を-∞から∞まで積分したら1になるんですね。

それは、確率を表すようにした関数なんですから、とりうる値の範囲すべてて積分をしたら1になるのはそらそうだろうとは思います。

でも、実際積分計算して積分結果が1になるのを導くのは大学数学の話です。（ガウス積分というやつで、多分大学の1,2年生くらいに習うと思います。ちょっと覚えてないのですが、、、。）

でも、高校数学の範囲で何かこの関数について言えることもちょぼちょぼあります。

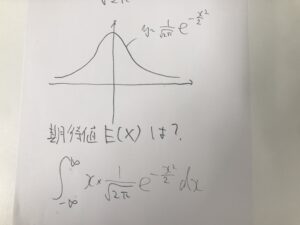
たとえば、期待値を計算で求めるとかはどうでしょうか。

積分の中身をf(x)dxでなくxf(x)dxにすることで期待値を表すわけですね。そうすると、

こんな式になるわけです。

高校数学の積分にある程度習熟している人であれば、ぴんと来ますよね。

 

そうですね。微分形がくっついているから元の形をひと塊として積分できるという置換積分が思い浮かびますね。

計算したらめでたく0になりましたね。（∞のところをあえて書きましたが本当の答案では書かないのが普通だと思います。）

まあ知られている結果が出ただけですが。。。

他にも、ちょっとだけ枝葉を切り落として積分の不等式と絡めて

こんな出題がありうるかもしれません。（またいつかブログのネタにします。）

いや、なんでこんな話を少ししているかというと、

統計自体は基本的に数2Bで出てくるものなんですね。

でも数3と絡めた題材が少しだけ盲点になるのかもしれないなと思って、そんな話をしてみました。

おしまい。