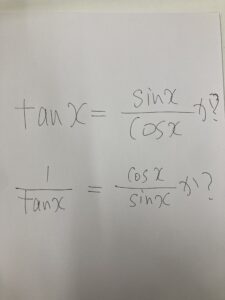素朴な疑問に大事な気づきが。

松谷です。

素朴な疑問から大事な気づきを得て、しっかり成長できるというときも結構あるかなと。納得感を得ることができて、成長実感を得られるいうか。

今日眺めていた問題のなかで、次のような内容にあたるときがありました。

基本中の基本だとは思います。

 

でも、その問題では、そこの理解が危ういと答えがとても怪しくなってしまうという問題で、改めてあ～こういう素朴な内容大事だなと思うに至りましたね。

 

結局、上は正しいのですが、下は正しくないのです。

正確には、常に正しくはないというか。定義域が違うわけですね。

1/tanxはたとえばx=π/2を代入できないのに対して、右側にはしっかり代入できて0になるわけですね。（左はx=π/2+πkを代入できない）

左側にもx=π/2にかぎりなく近い値を考えて、分母が∞に発散するから、結局0に収束するということは言えたとしても本当に0なのかと言われれば口をつぐむしかわけないですね。

もし、cosx/sinxを1/tanxに直すときがあったとしたら、注意を少し払ってあげなきゃなと。

そんな気づきが得られるかなと。

あとは、これは新しい学びなのかどうかはわかりませんが、懐かしいものに遭遇したしました。

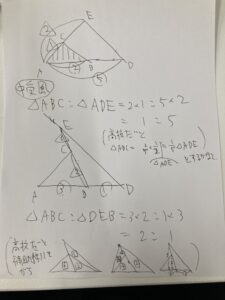
何か高校数学の図形の問題の質問を受けていたら、解説が中学受験風の解き方をしていて。なつかしいワードを想起することがありました。「りんぺん比」というワードです。

どの内容のことを「りんぺん比」と名付けているのかは実はよく知らないのですが、、、。りんぺん比の漢字もよく知らなかったり。。多分、隣の辺なのかな。