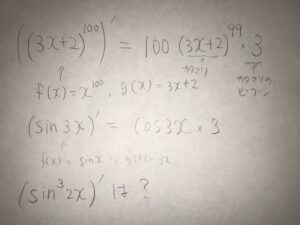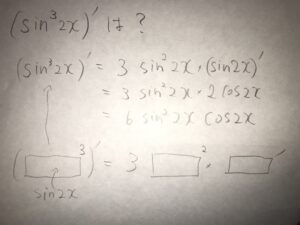一定の理解力とは合成関数の微分ができる力？

松谷です。

数3を教えていると合成関数の微分のところでつまずく生徒が一定数います。

稲荷塾くらいハイレベルな生徒層を集めていても1〜2割くらいいます。

合成関数の微分のルール自体はしごく簡単で、

f(g(x))の微分はf'(g)g'(x)となる。

つまり、g(x)をひとつの文字かのように微分して、その後、かたまりとして考えたg(x)の微分をくっつけるだけです。

で、このルールを理解して適用するだけなんですが、これまでの経験上はこんな風な生徒群に分かれます。

本を読んで問題演習を少ししただけで理解できる群、本を読んで演習をしてかなり間違うなかでコツをつかんでいく群、本を読んで演習をしてもなかなかわからずテストをしても間違いでもコツを頑張って伝えることでできるようになる群、どれだけ丁寧に説明してもなかなか正確にはできるようにならない群

に分かれます。

で、この理解力はかなりの程度大学受験時の数学力と相関しています。経験上は。

もちろん、ただの計算なのでいつかはできるようになります。

それは間違いありません。

ただ、できるようになるまでの時間が個人によってものすごく差があるんですね。小学生とか高校生とか関係なく。

特に、最後の生徒群についてはなぜそうなっているのかがとても気になっていて、個人的に解明したいと思っているんですね。

今の仮説は合成関数の微分は同時に２つのことを少し記憶にとどめながら操作するイメージなので、もしかしたらその作業ができないのかもしれないなと感じています。イメージとしては、繰り上がりの足し算をくり上がりをメモしなければ計算できないというイメージですね。もちろん、何がf(x)で何がg(x)なのかを全部かいて公式に当てはめて解くことはできますが、それではスピードも出ませんし、高いレベルには達しません。

まあ、東大京大医学部を目指す塾という生徒層からいうと普通は対象外であろう生徒たちなんだと思いますが、単純に個人的に気になるんですね。もしかしたらその作業力を鍛えれば逆に理解力計算力が高いレベルに達するかもしれないからですね。

まあ、僕がただあきらめられないだけですね。まだまだ理想だけを追い求める若手だということなのかもしれませんね笑（きっぱりと高校数学を高いレベルである程度短期間で学習するのは無理です。と伝えることも姿勢として間違っているわけではないと思います。）

もちろん集団で進める場合は他の生徒の不利益になるので、その生徒たちにより多くの時間をとるわけにはいきませんが、個別で質問対応する場合はしっかり頭の中の動きを解決してあげたいと思います。

ちなみに、上であげた混乱層が必ずといっていいほどできない問題の答えはこれですね。