算数か中学数学の空間図形の問題?
松谷です。
たまには、クイズ的に数学っぽい問題の話題を。
算数か中学数学の空間図形の問題について書いてみます。
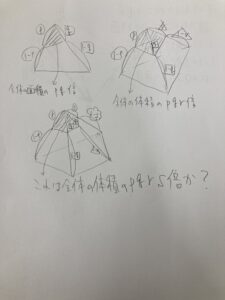
上のような問いですね。
中学受験のかなり難関中の算数で扱うか、高校受験の難関高校で扱うか、大学受験の難関大の問題として扱うかといった題材です。
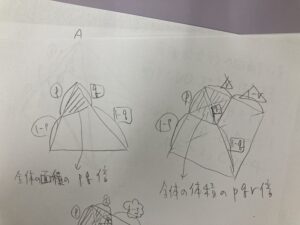
三角形であればpq倍になるのは比の考え方で一発でわかると思います。
四面体(三角錐)については少しだけ戸惑う人もいますが、
例えば左の側面を底面と見たら、底面積がpq倍になっていて、高さがr倍になっていることから、pqr倍になっているのはすぐわかるんじゃないでしょうか。
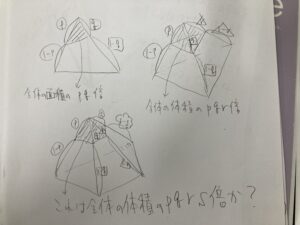
そこから一般化して、四角錘の場合もpqrs倍になるんじゃないか?
というのが今回の趣旨ですね。
こういうように一般化が成り立つかどうかを考えるのは大事なことだと思います。
で、まあなんとなくうまくいきそうな気もしますよね。
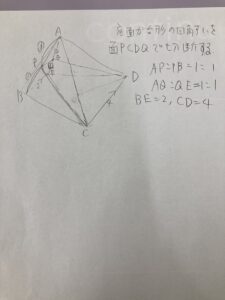
では、適当に一つ例を考えてみます。
計算が鬱陶しいと嫌なので、底面は台形にしました。出てくる内分比も1:1にしました。
しかも、一部は内分さえされていない簡単設定。
でも、まあもし予想が成り立っているとするならば、上側の体積は1/2×1×1×1/2=1/4倍になるはずですよね。
で、まあ実際に計算してみましょう。四角錘ってやっぱり少し考えにくいんですね。
多面体については四面体(三角錐)が一番基本となる図形だと思いますので、それに分けてあげるのがいいかなと思います。つまり底面の対角線で切るみたいな感じですね。
そうしたら、
あ、面倒くさくなってしまったので、解答を紙に書きました。。
どうやら計算してみると全体の5/12倍になっているようですね。
つまり、1/4倍という予想が不成立!!反例は一つでもあればもうその公式は破綻していますので、ということですね!!!
たまには、パズルっぽい?問題でした~。
(まあ適当に考えた問題なので、計算間違いしてないといいけど。。。)