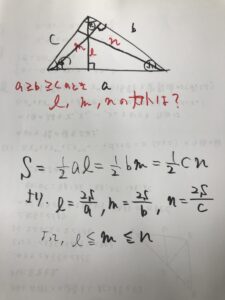三角形の辺がa≧b≧cのときの角や垂線の長さ。
松谷です。
たまには、算数数学の話題を。
中学か、高校くらいの内容でしょうか。
一般的に三角形が与えられていて、その辺をa,b,cとします。
このようにa,b,cという文字に対して条件的な優劣がなく、対称な条件となっている場合は、
自分で仮に大小を設定してあげるのは有力です。(あとで大小関係をはずしたり、はずさなかったり)
で、
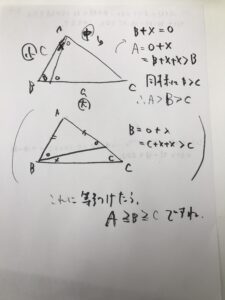
a≧b≧cのとき
その向かい合う角A,B,Cの関係はどうなるでしょうか?
そう。
実は、A≧B≧Cとなりますね。
簡易の証明は、こんな感じです。
ほうほうって感じですかね。
当たり前のことをいまいちど確認するという感じですね。
では、ついでに、辺の大小とそれに付随した角の大小が、
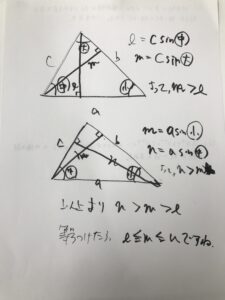
a≧b≧cでA≧B≧Cのとき、各頂点からの垂線の長さの大小はどのような関係になるでしょうか?
多分、こうでしょって予想つきますね。
a≧b≧cと、共通辺からのsinを考えたらわかりますね。
垂線の長さはl≦m≦nと真逆の関係になってますね。
いやいやおっさんごまかしているやろ。ちょっとA鈍角の場合とかでも本当にそう言えるんかいな。
sinは90°までは単調増加だけれど、そこから下がるからわからへんやんみたいな。
まあ、大丈夫なんですね。
よし、言えた!
Aとπ-AとB+Cのsinが等しいというのはたまに使うような。使わないような。
よし!言えた!
高校数学万歳!と思ったんですね。僕は。
ここで問題をもう一度見たときに寒気が走りました。
この問題は高校生の問題じゃなかったんです。
ただの、小5の問題だったんですね。。。
難しくかかなければ、面積が一定で、どこを底辺とみるかだけだから、底辺の長さの逆になるだけなんですね。
小学生の問題をここまでこねくり回して考えてしまった自分にびっくりしてしまいました。。。
穴があったら入りたくなってしまいました。。。
まあ、でも、強烈に記憶に残ったので、二度はしないと思いますが。。