radical plane?根面?
松谷です。
radical plane ってなんだと思いますか?
カタカナで書くと、ラディカル プレイン。
ラジコン飛行機か!
と思った方。
惜しいです。
いや、惜しくないか。
全然違いました。
radical planeは数学用語で、「根面」と訳されることが多いようです。
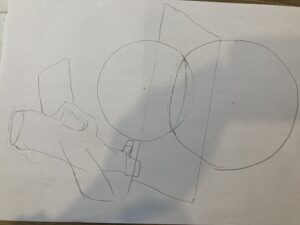
こんなやつです。左側はラジコン飛行機のつもりですが、、、そうではなく、、、絵心もおいておいて、、、、
右側の球と球の交わりである円を含む平面ですね。(まあ球どうしが交わらなくてもいいですが)
これを根面というんですね。
いやまあ根面という言葉はほとんどの方がきいたことがないかなと思います。高校数学で出てきませんから。
でも、これは次元を落としてやると、見慣れた構図になります。
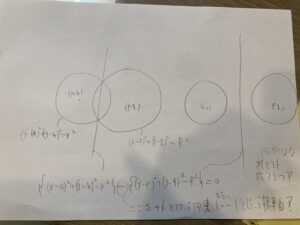
つまり円と円の交点を通る円や直線です。「円束」の話ですね。
伝統的な書き方では、{(x-a)^2+(y-b))^2-r^2}+k{(x-p)^2+(y-q))^2-R^2}=0
という方程式が、2円が交わる場合、kをいろいろ変えることで交点を通るいろいろな円たちを表せるんでした。(パラメータがついている方の円だけ表せませんが。)
ただし、k=-1にした場合だけ、x^2やy^2の項が消えてしまうので、円を表さず交点を通るという情報だけ残るので、交点を通る直線になるのでした。(直線は半径無限大の円ともいえますが)
その直線のことを「根軸」というのでした。radical axisと英語では言われます。
ちなみに、根軸は実際は二円が交わらない場合も直線の式になりまして、それらは、二円の接点までのの距離が等しい点の集合を表すんですね。
そして、根面の式もまったく同じように出てくるわけですね。
{(x-a)^2+(y-b))^2+(z-c)^2-r^2}-{(x-p)^2+(y-q))^2+(z-s)^2-R^2}=0
みたいな形でね。
まあなんとなく数2Bの授業の内容と別途受けた質問が交わったので、その交わりを記事にしました。一種の根面?ですね!