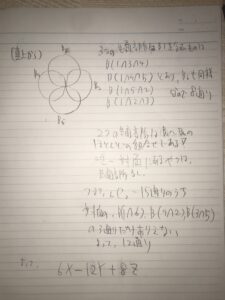眠れぬ夜は数学を(2022早稲田理工第4問)

松谷です。

受験前日の高3生が１つ質問してきていたので、不安のなか頑張っているんだなというのが感じられて、こちらもなんだか眠れません。

こんなときは、数学の問題の解説でもしてみるしかないですね。

こんな問題が今年の早稲田の理工に出ていました。

まあ、あんまり見えないと思うんですね。(1)をちょっと手書きで拡大するとこんな感じです。

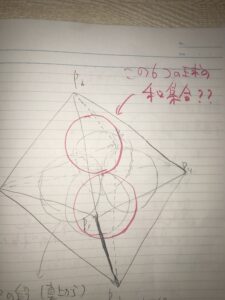
つまり、正八面体の一つの頂点を除く5点でできる四角錐の各面に内接する球が6つあります。

その球の和集合の体積を求めよと。つまり、それぞれの球をB1〜B6として、B1∪B2∪B3∪B4∪B5∪B6の体積を求めよということです。

ただ、実際に値を出すのは大変なので(1)では、各球の体積をX、2球B1とB2の共通部分をY、3球B1とB2とB3の共通部分をZとして、X、Y、Zで表せという問題になってます。

うーん、こういうとらえづらい立体はいろんな方向から見て見やすい方向をその都度選んでやるというはひとつの大事なコツです。

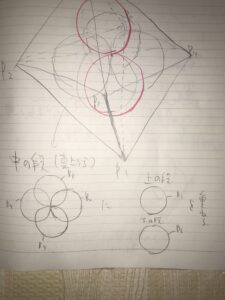
真上から見ることで中段が4つであるということがわかりやすくなります。

これで、とらえきれなければ、例えば、真横からの図を考えるこので、上段1つ、中段4つ、下段1つが結構わかりやすくなりますね。

そんな見方をするなかで、この問題のポイントとしては、4つ以上の共通部分がない！というのを掴むことかなと思います。

そうすれば、いつもの3つバージョンのベン図のごとく、

体積が、葉っぱを3枚引いて中の曲がったアイロンみたいな？やつを1枚足すような感じで計算すればいいとわかります。

 

とはいえ、結構複雑なんですね。

3つの重なりのケースは中段どうしでは無理なので、B1を含む場合を考えてから、B6を含む場合を合わせて２倍するのがよいでしょう。

2つ重なりのケースは対面の場合だけを除くといいでしょう。

そんなこんなの考察を経て、６x-12y+8Zということがわかるわけですね。

一応、僕がこの問題を見たときにすぐ思ったのは6文字のバージョンの包除原理？！それはきつくないか、ということでした。。

事実書いてみるのはスペース的にもかなりきついですね。。4つ以上がないと気づけばまあ、なんとか答えを書ききることはできますけどね。まあ、上のやり方と根本的には一緒かなあ。全体を数えてゼロになるやつを検討して引くのか、ゼロにならない奴だけを数えるのか。

そんな感じですね。

 

なかなか難しかったです。

僕としては今年の問題で1番難しいのかなと。

 

ちなみに、球B1とB2の体積の共通部分を求める問題や内接球の半径を求める問題が(2)、(3)にあったんですが、これの方が僕は考えやすかったです。

入試でみたら混乱しやすい問題ですね。

 

あっ、眠くなってきました。笑

 

おやすみなさい。