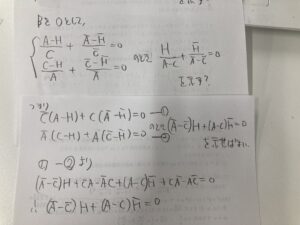簡単な道具だから簡単にできるとは限らない

松谷です。

なんとなく生徒目線で考えたとき使いやすい道具とか使いにくい道具というのがあると思います。

 

このまえ質問された複素数平面の内容に垂心の証明があったんですね。

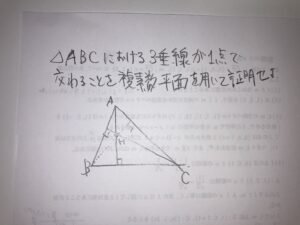
三角形の各頂点から対辺に向かって引いた3本の垂線が1点で交わるという証明ですね。

AからBCへの垂線とCからABへの垂線の交点をHとして、

BHがACと垂直であればよいという証明が一般的かなと思います。

 

ベクトルであれば内積0を示しにいけばいいでしょう。別に座標をおいても楽にできます。

 

でも、今回は複素数平面でということですから、垂直条件は純虚数条件と対応しますね。

ということで、2種類くらいの解答が思い浮かぶと思います。

つまり純虚数をkiとかそんな風に表現して普通に計算して処理する。

もしくは、純虚数条件をZ+Zバー=0の形で使っていくみたいな感じです。

で、普通生徒は最初上の解法がとっつきやすいと思います。

ただの計算に落とし込めるので。

とっつきやすい簡単な道具でしっかり計算して解答する。これも

もちろん悪くありません。

 

しかしながら、簡単な道具が必ず簡単な解き方になるとは限りません。

実際この問題の場合、後者の道具を使った方が楽かなと。

分母を払って単純に引き算するだけですしね。

 

高校数学で紹介されるような道具は当然どれも使い道があるものです。

最初はとっつきにくくても、実は有用だということはしょっちゅうあるわけなんですね。

 

ちょっと使ってみるうちに、おっこいつ案外かわいいいやつだな！

と思えてきたりすることもあるかなと思います（笑）