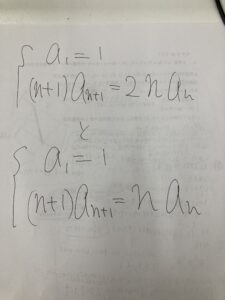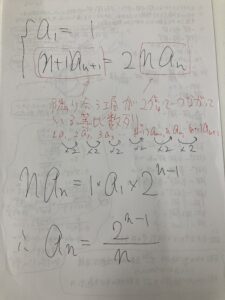簡単なものの方が難しく見えることもある

松谷です。

数学の問題の中では、

簡単な見た目のものの方が逆に難しいと感じることもあります。

これとかどうですか？

上と下どちらが簡単に見えますか？下の方が簡単に見えるんじゃないかなと思います。

しかし、生徒にやらせてみると上より下の方が出来が悪いことが多いような気がします。

 

上の問題でも下の問題でも、na_nという大きなかたまりをひとつの数列とみなすところは一緒です。

で、上の問題は、

隣り合う項が２倍で結びついているから、公比２の等比数列になるわけです。

漸化式は、基本の等差数列、等比数列、階差数列のどれかに帰着させるのが基本になるので、ある意味基本の形そのままなんですね。

でも、

この下の方の式は、なんなんだ？

と思うわけですね。

 

何数列なんだと？

 

これは公比１の等比数列とも言えますし、公差0の等差数列（ある意味階差数列）とも言えます。

つまりもっともっと原始的な式だったがためにわかりにくかったわけですね。

「隣り合う項が常に等しい数列」ととらえれば良かったわけですね。

 

分かってしまったあとの人にとっては、なんだ簡単すぎるから問題にもならないんじゃないかと疑心暗鬼になってしまうような問題なんですが、実際には結構ひっかかるんですよね。

実際小テストで急遽この問題（をもう少しだけ複雑にしたやつ）を差し込んだのですが、何人か躓いていたので、成長の機会を与えられて良かったなと。

テストとかで必死に考えてできたときとか、テストとか痛い目を見たりしたときとか、それら両方が記憶にすごく残りやすいんですよね。

講師とかが一生懸命力説するよりね。