見えにくいものを見ないで済ます？見ようとする？

松谷です。

空間図形って想像つきにくいことがあるんですよね。

そういうときに「注目したい平面を取り出す」という定石があります。

たとえば正四面体における対称面とかが有名な話でしょう。

他にも、回転体を考えたいときにもわかりにくいときがあります。

わかりやすいものならいいですよ。

回転軸と同一平面内にある図形であれば、多少複雑でも想像つきます。

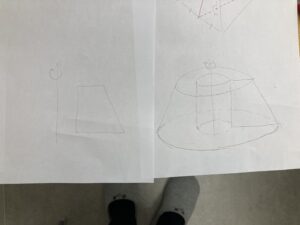
たとえば、これはどうでしょう？

これは、そうですね。

円錐台から真ん中の筒をくりぬいた感じですね。

本屋さんにある店員さんが立って本とるやつが健康用に少し穴空いてる感じですかね。。？

しかし、同一平面にないやつならとたんに考えにくくなります。

例えば回転軸とねじれの位置にある直線とか、回転軸とねじれている三角形とかね。

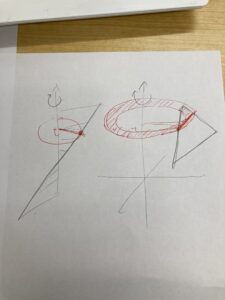
そんな場合は、「切ってから回す」という技が効果的なわけですね。

 

そして、さらにわかりにくいものとしては、

立体を回転させるなんて話があります。

これが結構分かりにくいんですね。

例えば、直角三角形を回転させたら、円錐なんてさっとできうるのに、そんな単純な図形であっても、それを回すとなるとちょっとわかりにくくなります。

 

そういうときに、数式的に扱いたければ、

やっぱり「切ってから回す」のが有効です。

円錐曲線の知識があれば、母線に平行な平面で切れば切り口は放物線に、

そうでなければ双曲線になったりします。その式を求めてから回すというのはとてもいいでしょう。いや、それすらもせずに、回転軸から最も近い点と遠い点に注目することで処理できてしまうともいえます。

はっきりいって立体の形を一切考えずに積分して体積などを求めることができます。

 

しかし、見えにくいからといってまったく考えないでいいかというと、

そういうわけではないときもあるかなと思います。

 

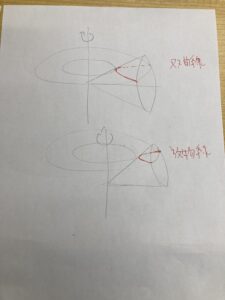
円錐を回した形は実際よく考えてみると、

母線の長さが一定で、

中心からの距離が一定のものを回すと考えると、

 

そうですね。球にになるんです。そこから一部がくり抜かれた形になるんですね。

 

 

みえないものでも少し想像してみる。

そうした先には何かが見えることもありますね。

対称性とか、ある図形が浮き上がってきたりとか。

そういう思考が機械的な解法一択より楽な解法の選択につながったりすることもあるのかなと。

まあ機械的な解法は身に着けてもらうとしてね。