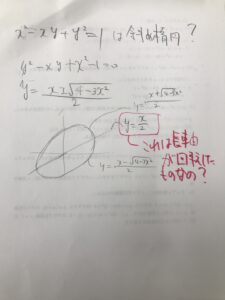アステロイドの謎?に迫る
松谷です。
ちょうどアステロイドの話を少しこの前の授業でしたんですね。
長さaの棒をx軸とy軸に沿って動かしたときに境界にできる図形だよ。
とか
パラメータ表示がx=acos^3θとy=asin^3θだよ
とか
実は半径4対1の内サイクロイドだよ
とかそんな話をしました。
で、時間があまったら、棒を動かしたときなんでそんな曲線がでてくるかって問題をやってもらおうかなと思ったんですね。
で、そんな時間はなかったので、無理だったんですね。
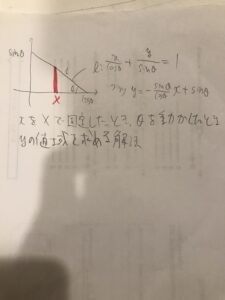
で、この通過領域の求め方は、線分の通過領域なんですが直線の通過領域を考えてx軸とy軸で切り取って考えていきます。
で、そこからなんですが、
一般に順像法とかいう文字固定でのやり方(ファクシミリの原理と読んでる雑誌もあります。ファクシミリ誰も知らない時代ですが。。)が紹介されています。
本によっては、それじゃないと厳しいというように書いてありました。確かにその解き方でさくっと求まります。
しかし、普通通過領域系統の問題であれば、(x,y)に対してパラメータの存在を考えるのが普通に最初考えることかなと。つまり、逆像法という考え方です。
でまあ、確かに、分母を払ってきれいにしてから
こんな感じでやると処理不能に陥ります。
でも、完全に分母払わず両辺にsinθだけかけるだけの変形だと
めちゃめちゃ簡単に求まるんですね。
うーん、なんで、この解き方が主流の一つとして紹介されてないのかなあ。
はて。
ちなみに、だいぶ昔ですが阪大の10年くらい前の理系数学にこれの類題が出てたかな。早稲田もあったような。ちょっとうろ覚えですが。
そんなことをふと考えた日曜でした。
動物園でカバを見たり、わたあめを食べたりしながらですが。
カバは水から出てて干からびそうでしたね。。