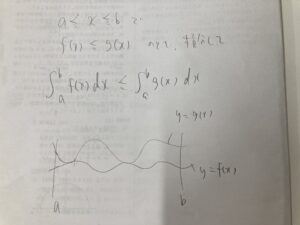数学講師バカ問題を作ってしまう

松谷です。

数学を教えていて、やや難しい問題を教えるときに、生徒がすぐ理解に到達しなそうだなということがあるんですね。

そういうときは、即興でその要素を含みながらだいぶブレイクダウンした問題を作ることがあるんですね。

しかし、伝えたい要素につい集中してなるべく基礎中の基礎の要素だけにと思った結果、バカ問題を作ってしまうということがありました。

それがこれです。

まず、僕が説明したいなと思った内容は積分の不等式という範囲でした。

これは結構高校生にとっては難所で、最初難しく感じるんじゃないかなと思います。僕も最初難しく感じたというか、受験時にはたいしてわかってなかったんじゃないかという気もします（汗）

しかし、実際の要素としては、極めてシンプルで、

これだけなんですね。

ある範囲(a≦x≦bなど）で関数の不等式があったら、その範囲で定積分してもそのまま不等式が成り立つ。（等号は関数がその範囲でずっと一緒のときだけ。）

ただ、問題を解くときには、ちょっと宝探しみたいな要素があるんですね。

積分区間や目標やグラフなどがヒントになって関数を見つけるみたいな。

つまり、どういうことかというと、

 

こんな感じですね。

まあそれで0~1区間においては、xは指数が大きくなればなるほど小さくなっていくから、

x^3≦x^2≦xではあるな。グラフかいてもx→x^2→x^3とたわんでいく感じになっていてこういうのも大事な視覚的ヒントになってたりもします。

そして、思いついたこの関数を0~1区間で積分してみると、ちょうど1/4と1/2になる！

これでいいんだ！！！やった！！

 

 

みたいなね。

 

 

10秒くらいで作った問題にしてはなかなかいいんじゃないかと思ったわけですね。

 

 

 

しかし、、、、

 

 

 

そう、これは致命的なバカ問題だったんですね。。。。。

 

真ん中の積分がすぐ計算できてしまいますから。。。。

 

いやいや、もし、その計算ができないとしたら、この考え方にも価値があるじゃないかという言い訳が1秒くらい頭をよぎりましたが、、

 

いや、それ計算できなかったら、x^3の積分もxの積分も無理やから、、、不等式示せないわけですね。。。。。

 

 

真ん中が高校数学範囲で積分が結構厳しいときに、それを積分計算しやすい関数ではさめたときに、この積分の不等式の考え方より有用になってくるんですね。。。。

「それも学べて良かったね！」ということにしました。。。。。