4つバージョンのベン図？

松谷です。

ベン図ってありますね。

たとえば、1~100までで2の倍数か3の倍数である数は何個あるか？

みたいな。

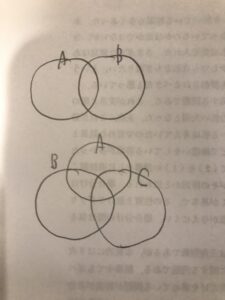
それを視覚化するときにベン図が便利ですね。

2つとか３つの場合が頻出ですね。

特に、ＡとBの集合のどちらかに含まれるやつとか、

ＡとBとCの集合のどちらかに含まれるやつとかを考えるときに有効ですね。

こんな感じの図を考えたらわかりやすいですね。

でも、機械的に実は考えられるんですよね。包除原理っていって、公式があって、

P(AまたはＢ）＝P(A)+P(B)ーP(AかつＢ）

とか

P(AまたはＢまたはＣ）＝P(A)+P(B)＋P(C)ー{P(AかつＢ）+P(ＡかつＣ）+P(ＢかつＣ）｝+P(AかつBかつC)

とかですね。3つまでのやつは京大とか東大とかでよく出ますね。ベン図書けばいいですけどね。

さて、でも、4つのやつも機械的に考えたら、

P(AまたはＢまたはＣまたはＤ）＝P(A)+P(B)＋P(C)＋P(D)ー{P(AかつＢ）+P(AかつＣ）+P(AかつD)+P(BかつC)+P(BかつD)+P(CかつD)｝+{P(AかつBかつC)+P(AかつBかつD)+P(AかつCかつD)+P(BかつCかつD)}ーＰ(AかつBかつCかつＤ）

みたいな感じで求まりそうですね。プラスマイナスが交互にきて、１個のやつー2個のやつ＋3個のやつ-4個のやつみたいな感じです。

これが確か滋賀医大で出ていたような気がします。証明せよっていうのを誘導が与えられていて。難しかったと思いますが。

で、４つバージョンだと複雑すぎるからベン図もかけないし、この公式があるからいいなあと思う人が多いと思うんですね。

 

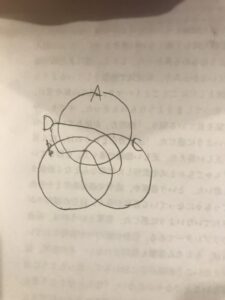
でも、実は4つバージョンのベン図かけるんですね。

なんかちょっと対称っぽくないから気持ち悪いんですけどね。

よく見ると確かに、重なり具合がAとBとＣとＤについて対等になっていますね。