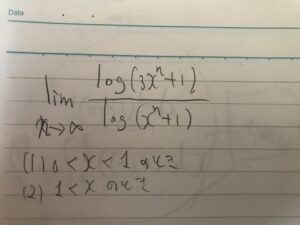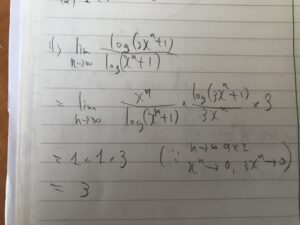つまりやすい極限と難問に相対したとき
松谷です。
年末にちょっとわからずに何日か放置していた問題の解答がふと2問連続で舞い降りてきましたので、なんとなく今年はいいことがありそうですね〜。
そんな何日も考えることはなかなか受験生には許されない贅沢ですけどね。
高2以下くらいはいくらでも時間ありますので、結構粘って考えるというのは娯楽と実益を兼ねてやってみるといいと思います。でも、考える道具がある程度揃ってないと意味ないので、早めに単元学習を終えることは大事ですね。
でも、高3生でも30分くらいは粘った方がいいかなとは思います。いざというときに粘れなくなってしまうので。また15分粘らない人は基本的に難問解けることはないです。
さて、最近出会った問題で案外高校生、受験生が詰まりそうな極限がありましたので、ちょっと載せてみます。
こんなのですね。
まあ、考えたい人は考えてみてください。高校生が見ているかは謎ですが。。
さて、答えとしてはこんな感じです。
はい、終わりでもいいんです。でも、極限の問題って答えを見てそうですかってわかっても、それを自分で出せるかっていうと結構怪しいんですよね。
なので、それが一瞬で思いつがなかった場合の思考過程の例を出すとこんな感じです。
つまり、不定形の確認と、極限を求めるときの知識の整理、あとどれくらいになりそうかという大雑把なイメージも大事だったりします。(無限の中の大小を意識したり、徐々にnを変えていったり。)
(2)での考えるためのイメージはこんな感じでしょうか。
で、まあ、そんなことを思い浮かべてから解答を作ると、こんな感じかなと。
イメージを作っておくと当然解答にも自信がもてますしね。
一応、もう一つ考えたはさみうちの原理でやっとくとこんな感じですね。これもごちゃごちゃと思考過程をかいてみました。
まあ、経験的には一般に受験生が苦戦しやすい極限は、はさみうちか、微分係数の定義を利用した極限ですしね。特にはさみうちで、自分で不等式を作っていくところが慣れないと少し式操作に躊躇してしまうんでね。
自分では難しいなって思った問題があって、解答に書いてあることは理解できたとしても、自分で本当に思いつくか?っていうところは意識して欲しいなと思います。
汚いノートの字をそのままですみませんが。。はは。
ではでは。本年もよろしくお願いします。