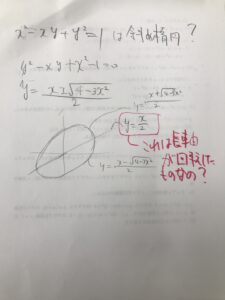斜め楕円の不思議

松谷です。

x^2-xy+y^2=1など普段の楕円や円の式にxyの項がくっついているやつは斜めの楕円を表したりします。

でも、斜めの楕円は少し難しいので、このグラフを書いたりするときに、

yの方程式とみて、yについて解いて、二つの関数のグラフに分けて考えるのが教科書などに載っている手法です。

で、この式だったら、y=x/2を境に上側と下側に分かれており、それを合わせて楕円という感じなんですね。

それで、このy=x/2って楕円の長軸を回転させたものなの？

という疑問が浮かびませんか？なんとなく？

 

 

 

で、どうかというと。。。。

 

 

違うんですね！

なんと！

実はこれ、普通の楕円を45度回転させたやつなんですね！

いつもの軌跡の求め方で逆回転させてあげればわかります！

ちょっと説明は面倒になってきたので、はしょりますが（笑）

つまり今回の斜め楕円の長軸はy=xになっているはずなんですね～。

（もちろんいろんなケースがありますよ）