気分は彫刻家

松谷です。

昨日みた問題にこんなのがあったんですね。

知識がいらないので誰でも楽しめる問題かなと思います。

 

これは高校入試なんですが、中学受験にもよくありそうです。大学受験としては、もうちょっと違う立体にするか、これを回転させたりするかとかそんな感じですかね。

あと実際は立体の体積や表面積を求める問題でしたが、立体をイメージできたらやりやすい問題なので、立体の図示をしてみたらどうですかね。体積は図示しなくてもできますが、表面積は図示することで、だいぶやりやすくなります。

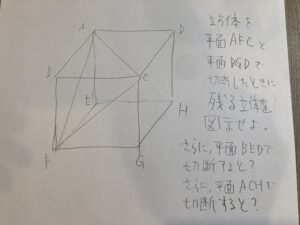
まずは、平面ACFに加えて、平面BGDでの切断を加えてみます。

うむ。

おー、なんか等脚台形がでてきて面白いですね。

ポイントは同一平面にある点をつなぐことなんですが、特に、真ん中の線をいれることがポイントですね。

平面と平面の交わりは直線の交線がでてきますからね！

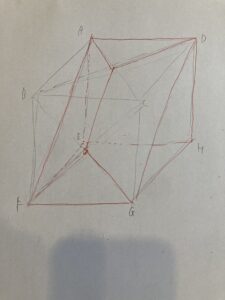
さて、さらに平面BDEの切断を加えてみます。

うおー、ちょっと綺麗ですねえ。ひし形が等脚台形にはさまれてる感じですね。面の切り方からみて、手前と奥が対称になって、左側が別の形になってるのは想像できますね。

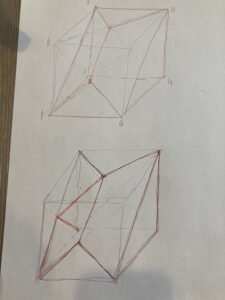
こうなったら、最後に平面BCHでの切断を加えたくなりますね。

おー、これで、四方向から対称にになりましたね。ひし形がら4つ出てきました。おしゃれなチョコレートケーキみたいな？！

 

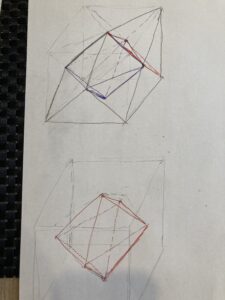
いやーここまでやったら、もしかしたら、8つの角全部削りとりたいですかね？

そしたら、おー、正八面体がでてきましたねー。ダイヤモンドみたいな！

すてきですね。立方体の中にダイヤが埋まってるみたいな！

正四面体の四つ角をとっても同じものがでてきますね。

 

しかし、僕がそこまで、詳しくないだけで、中受とか高受の超パターン問題なのかもしれませんけどね。。。。